Lagrange's Theorem

Theorem

Given a finite group \(G\) with a subgroup \(H\), then

\[ |G| = [G : H] |H|\]

Lagrange's theorem feels almost obvious once it has been proven that a group is made up entirely of non overlapping, equivalent sized cosets in a given subgroup. That is, when we split up a group in cosets we have something that looks kind of like this:

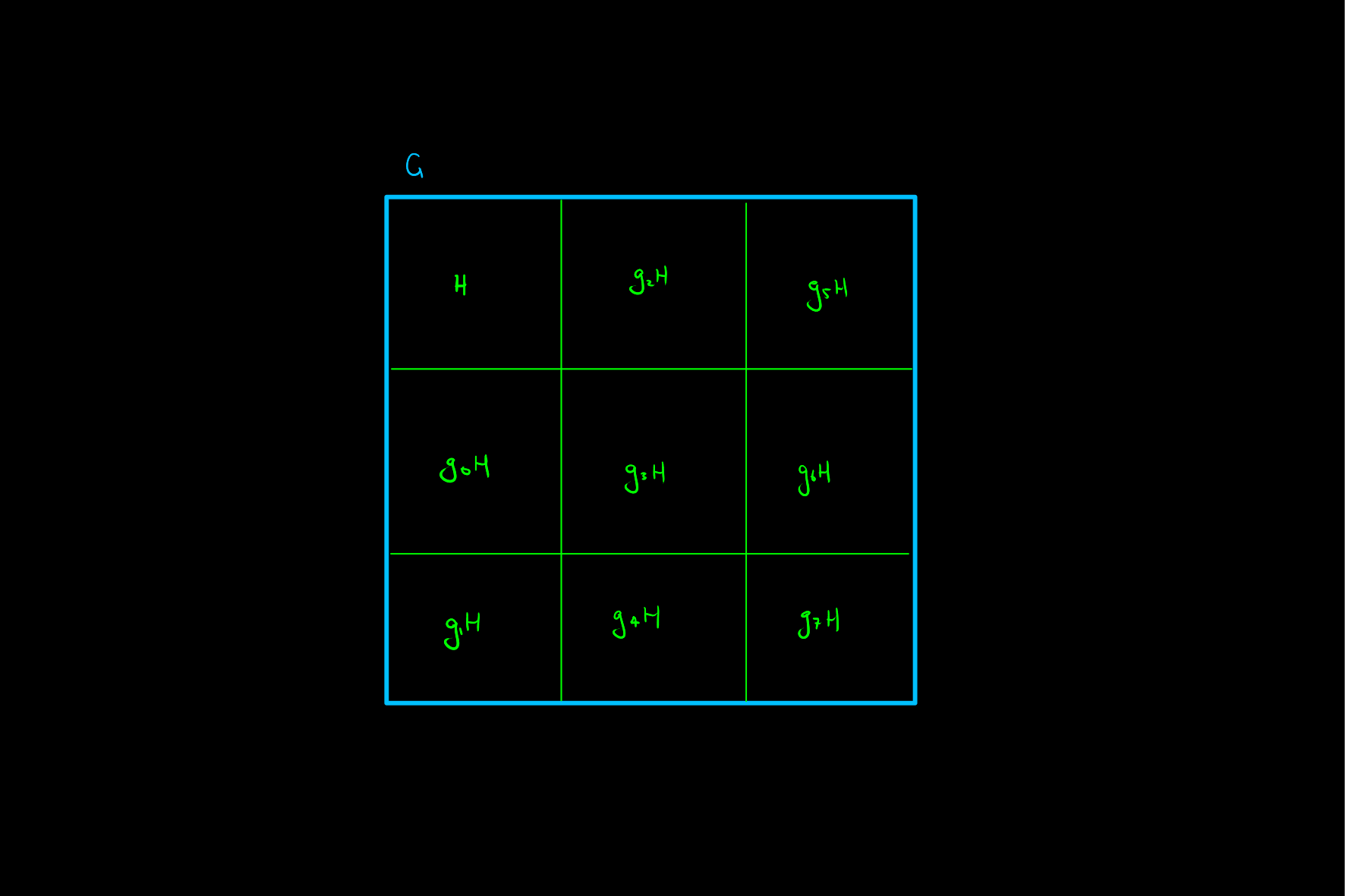
rather than like this, where cosets are of different size:

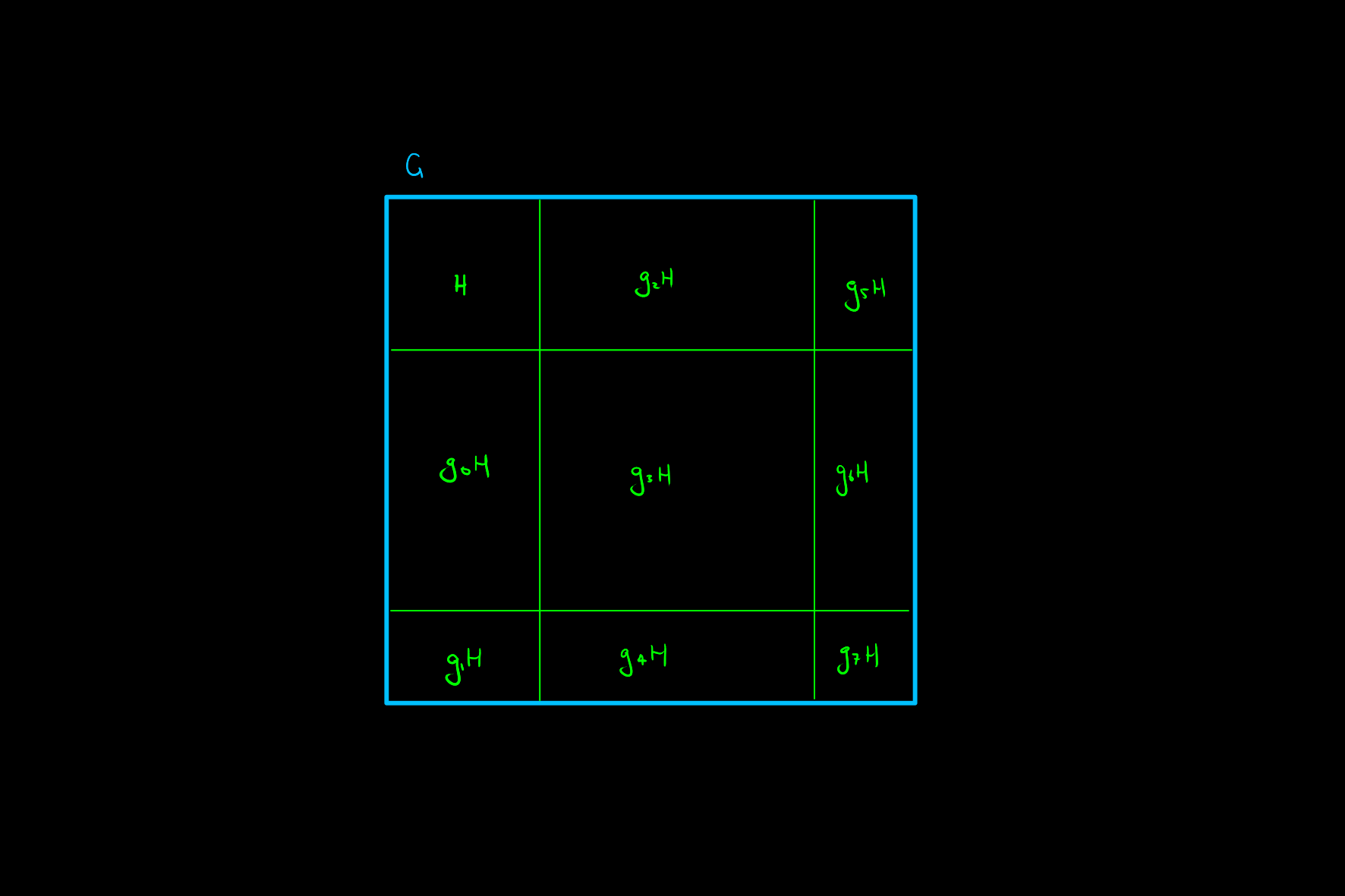
or like this, where either distinct cosets overlap or there are elements not in a given coset:

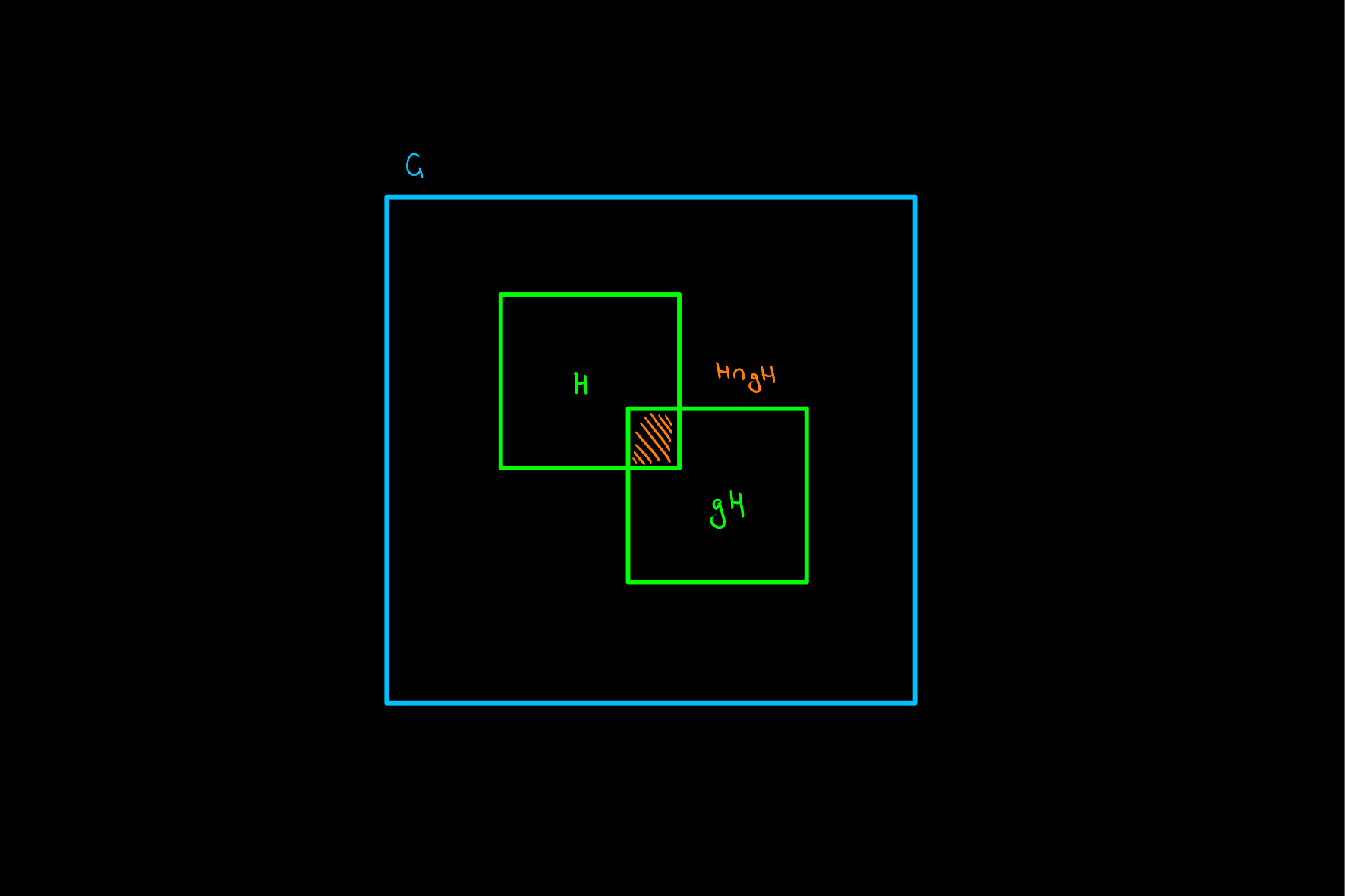
Proof

To prove this, consider the expression of \(G\) as a union of disjoint left cosets:

\[ |G| = \left| \dot\bigcup_{i = 1}^{[G : H]} g_i H \right|\]

Note that the indexing on the union is from \(1\) to \([G : H]\) as the index of \(H\) in \(G\) is the number of such left cosets. Then, proceeding algebraically:

\[\begin{align*} |G| &= \left| \dot\bigcup_{i = 1}^{[G : H]} g_i H \right| \\ &= \sum_{i = 1}^{[G : H]} |g_i H| \\ &= \sum_{i = 1}^{[G : H]} |H| \\ &= [G : H]|H| \end{align*}\]

Note that the conversion from union to sum is possible because the sets are disjoint, and the following line uses the fact that all left cosets have the same order as the subgroup itself.